MetaEditor

• 我们全面修订了 MQL5 Storage，用 Git 取代了 Subversion 作为版本控制系统。Git 是开发人员的全球标准，在代码管理方面提供了增强的可靠性和灵活性。
  
  
  • 灵活的分支和合并 — 为新功能或实验创建单独的分支，并将其轻松合并到主项目版本中。
  • 更快的存储库操作 — 与 Subversion 不同，Git 将所有数据存储在本地，大大加快了提交、版本切换和更改比较的速度。
  • 离线工作能力 — 无需持续的服务器连接：在本地提交更改，并在方便的时候将其推送到在线存储库。
  • 高级更改跟踪 — 轻松查看版本历史记录，跟踪带有时间戳和作者的修改，并恢复到以前的版本，而不会出现任何问题。
  • 卓越的合并功能 — 先进的比较和合并工具有助于最大限度地减少冲突，简化协作开发。
  
  协作开发迈上新台阶
  随着向 Git 的过渡，我们将推出 MQL5 Algo Forge，这是一个新的在线项目管理门户。它不仅仅是一个项目列表，它是一个面向开发人员的成熟社交网络 — 本质上，它是面向算法交易者的 GitHub。关注有兴趣的开发者，创建团队，轻松地在项目上进行协作。

  
  
  

  
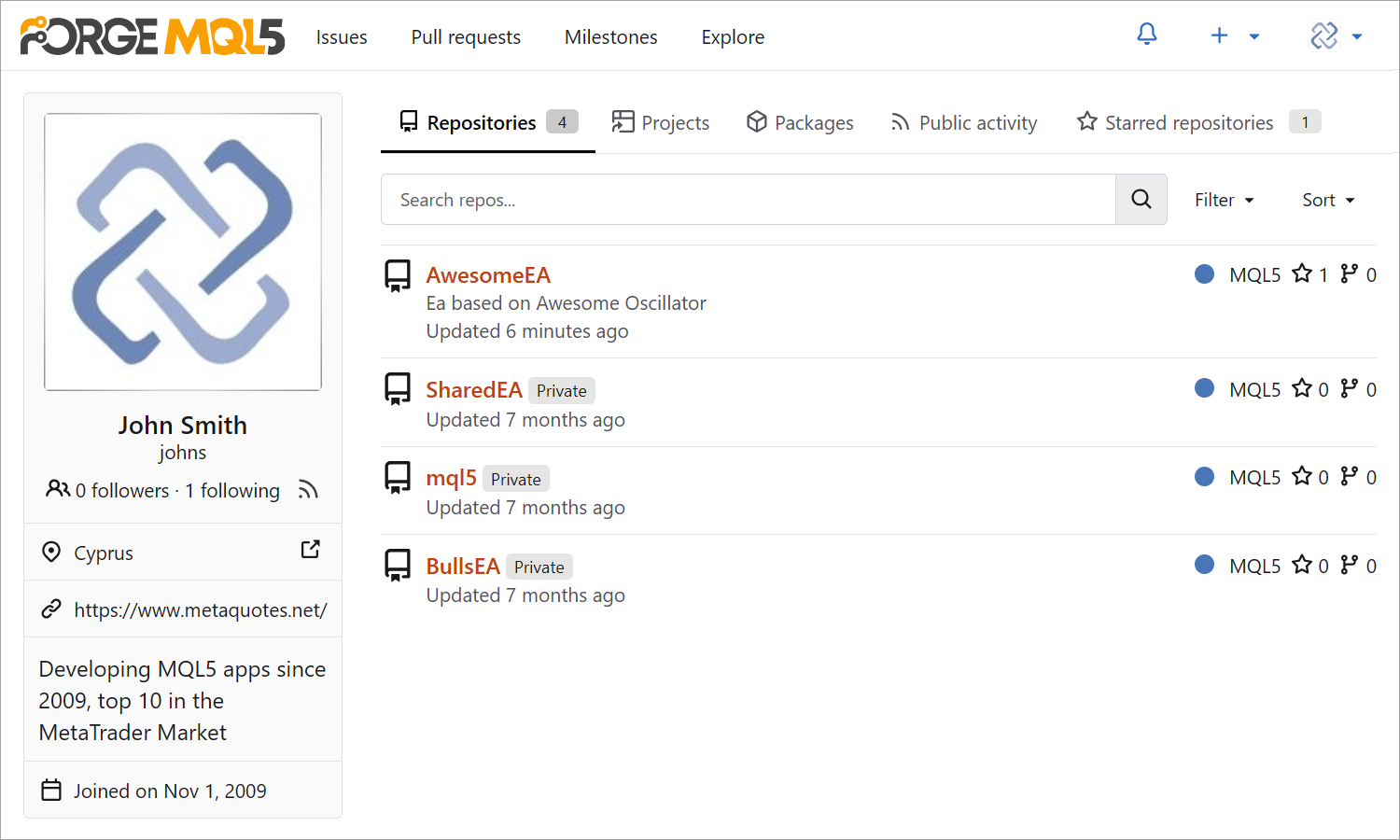
  查看项目详细信息：结构、文件、提交、分支等。跟踪个人贡献、创建文档和在线共享项目。

  
  
  

  
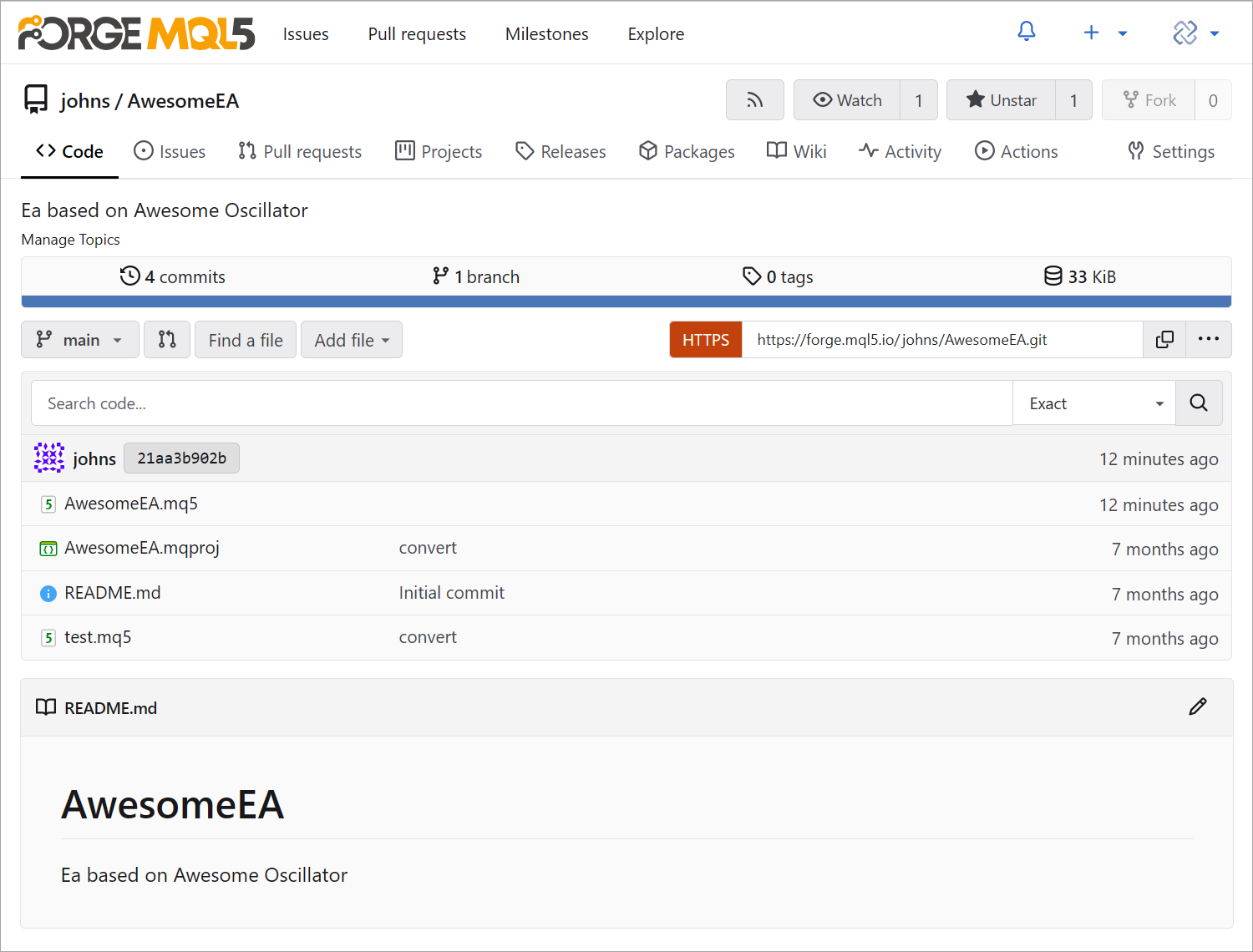
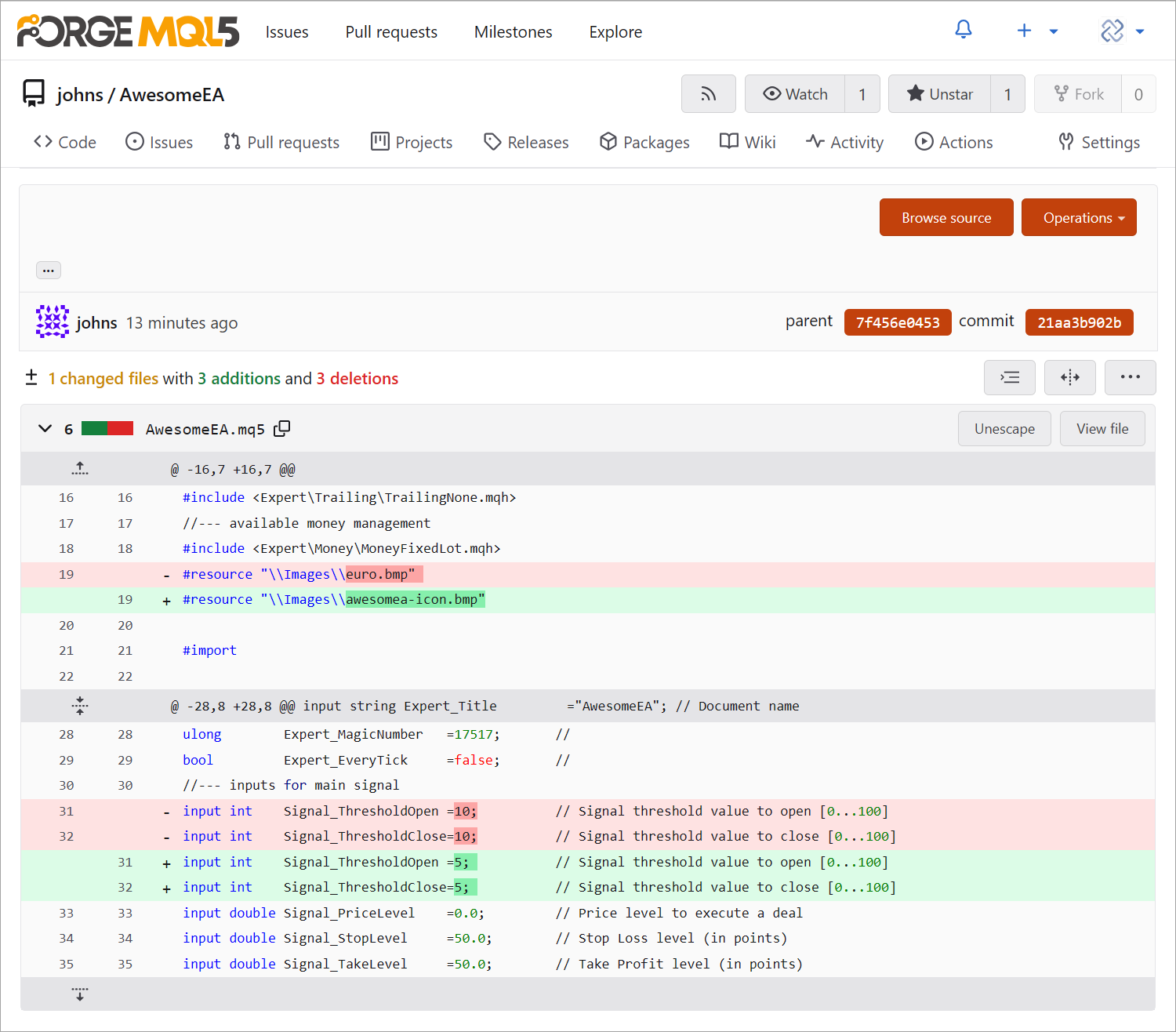
  监控所有代码更改：检测新的、修改的和删除的代码行。如果出现问题，直接在项目中向开发人员分配任务。

  
  
  

  
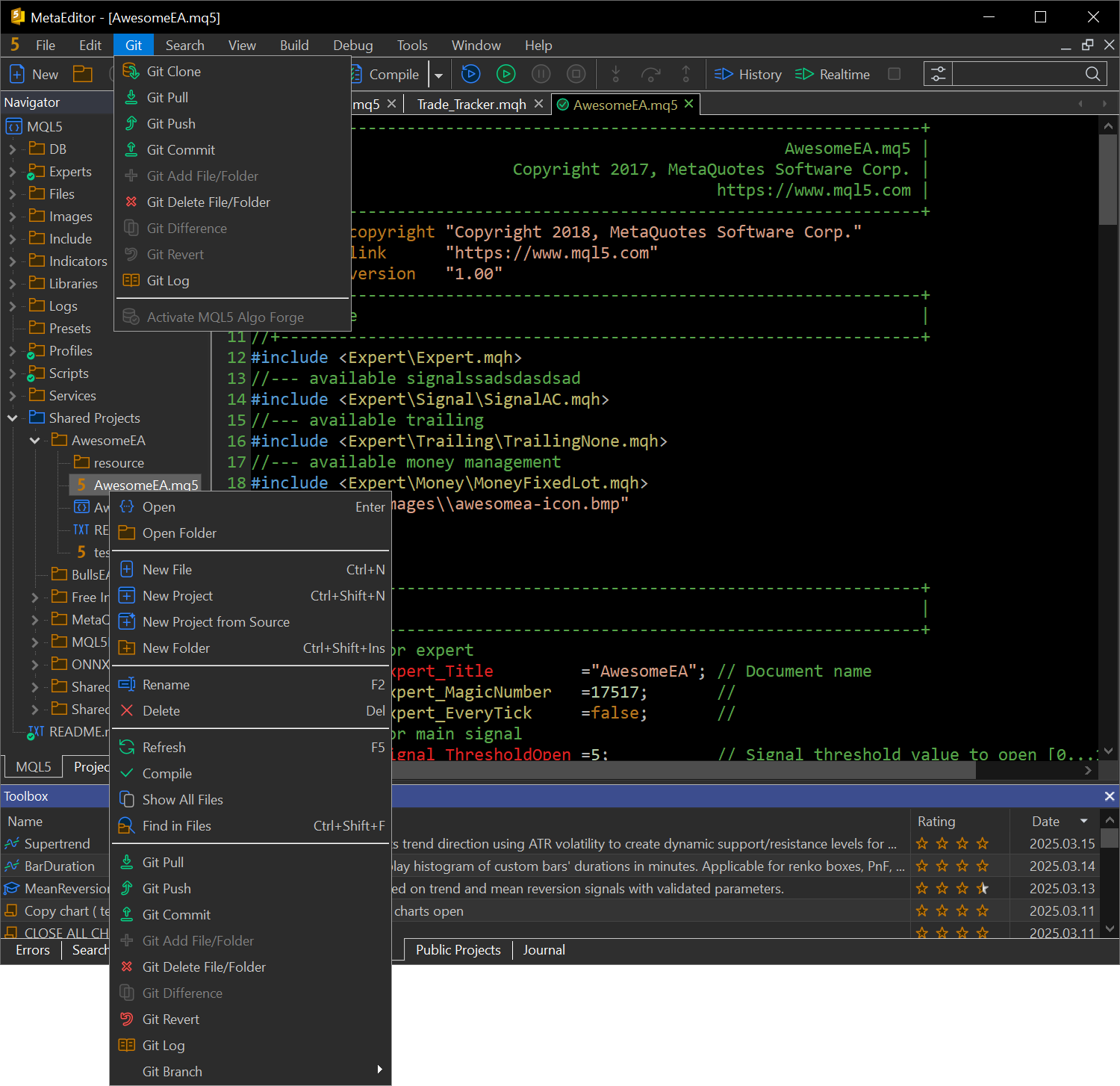
  为了提高 Git 的可用性，我们重新设计了导航器和活动代码编辑窗口。我们还在 MetaEditor 工具栏上引入了一个专用的 Git 菜单：

  
  
  

  
  全面的 Git 文档即将发布。
  
  

程序端

1. 为所有组件添加了对深色方案的支持，包括交易终端、MetaEditor 和可视化测试器。深色主题可在夜间提供更舒适的开发体验。使用 "查看" 菜单进行切换：

   
   
   

   
   在调整界面以支持不同主题的同时，我们还对对话框、菜单、面板和按钮的显示方式进行了大量改进，以提供更舒适的用户体验。在 MetaEditor 中，光标位置信息和文本输入模式指示器（INS/OVR）现在显示在右上角。取消了底部状态栏，以节省工作空间。
   
   
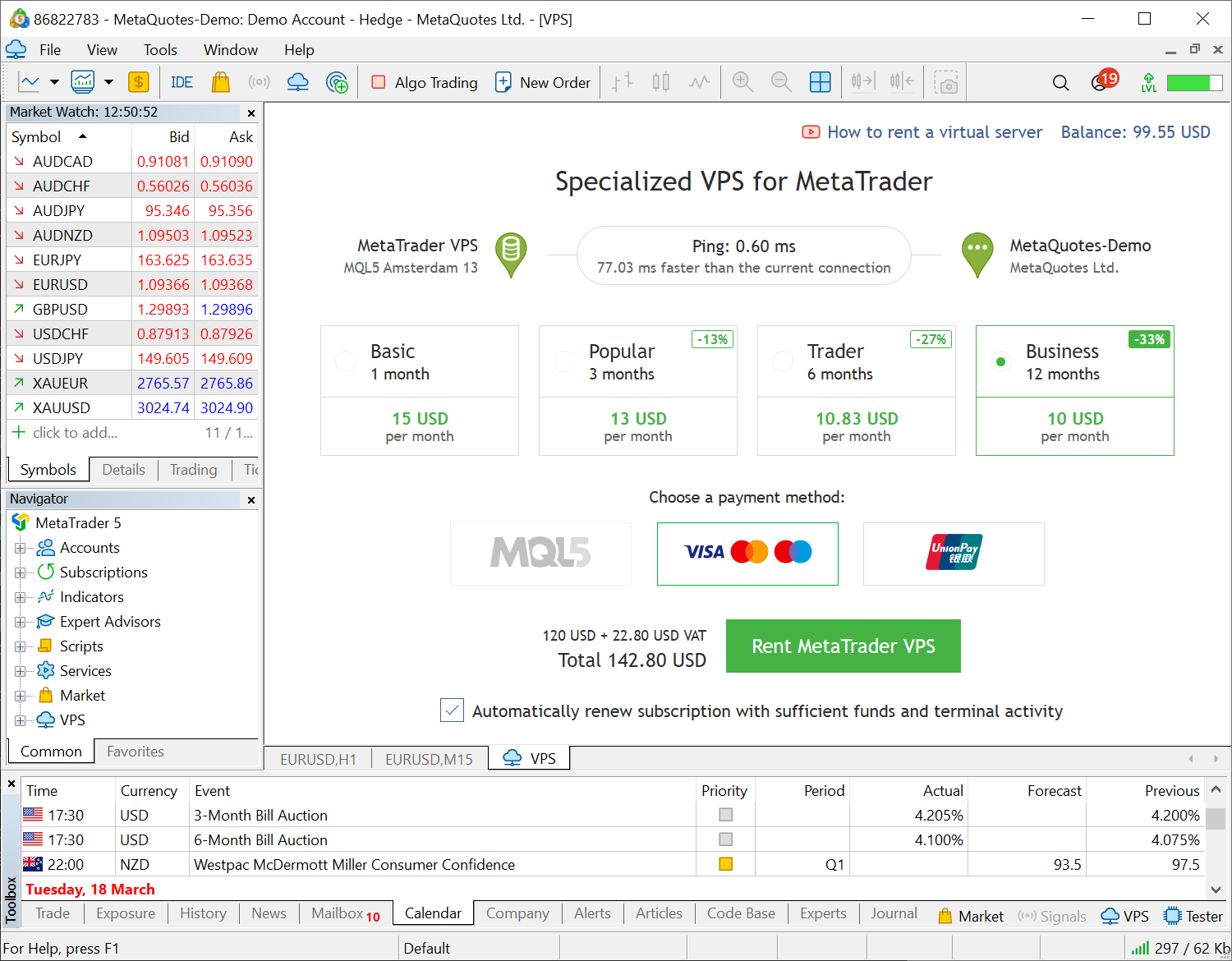
2. 新增 12 个月 VPS 租赁选项。通过提前购买长期托管服务，您可以节省三分之一的总成本。

   
   
   

   
   
3. 优化了内存使用。终端现在消耗更少的系统资源，从而提高了性能。
4. 优化了账户交易历史的显示。平台现在可以正确显示数百万条记录。
5. 在 "窗口" 菜单中添加了 "重置为默认" 命令。它可将所有界面元素，包括图表、导航器、策略测试器等，重置到原来的位置。
6. 修正了导致仓位修改对话框在某些情况下冻结的错误。
7. 修正了含有负价格未平仓位的数值计算。
8. 修正了保证金率计算在交易品种规格为负价格时的问题。
9. 修正了当前 MFE 和 MAE 值的计算，并在交易报告中显示其图表。
10. 修正了图表子窗口中振荡器的缩放比例。振荡器的垂直缩放现在显示正确。
11. 修正了全屏模式切换时订单簿和选项板的可见性问题。
12. 在账户交易历史中增加了仓位编号显示。使用快捷菜单启用相关列。
13. 修正了期货和期权 "风险 "选项卡上的清算值计算。
14. 修正了将新建账户数据复制到剪贴板的问题。在模拟或初步账户注册的最后一步，用户将获得账户详细信息：登录名、密码等。这些内容可以复制到剪贴板，保存到单独的文件中。相应的命令现在可以在 macOS 上正常运行。
15. 修正了 VPS 日志部分的显示。在某些情况下，页面可能会显示错误。
16. 修正了 Linux 上 HiDPI 显示器支持的问题。
17. 更新用户界面的翻译。

1. 添加了矩阵乘法运算符 @。它遵循线性代数规则，允许矩阵和向量的乘法，以及向量的标量（点）积。
   
   矩阵乘法（矩阵 × 矩阵）
   

   matrix A(2, 3);
   matrix B(3, 2);
   matrix C = A @ B; // Result: Matrix C of size [2,2]

   矩阵乘法（矩阵 × 向量）
   

   matrix M(2, 3);
   vector V(3);
   vector R = M @ V; // Result: Vector R of 2 elements

   矩阵乘法（向量 x 矩阵）
   

   matrix M(2, 3);
   vector V(1, 2);
   vector R = V @ M; // Result: Vector R of 3 elements

   标量乘法（向量 × 向量）
   

   vector V1(1, 3), V2(1, 3);
   double r = V1 @ V2; // Result: Scalar

2. 在 Std、Var 和 Cov 方法中添加了 "ddof" 参数。此参数定义了计算标准偏差时从分母中减去的自由度数。对于 Std 和 Var，默认参数是 0，对于 Cov，默认参数为 1。
   
   ddof 如何影响计算：
   
   
   • 默认情况下，ddof=0，表示计算总体标准偏差。
   • 如果 ddof=1，则该函数计算样本标准偏差，该偏差根据有限样本大小进行调整，这在分析数据子集时通常用于统计学。
   
   
3. 添加了新的 OpenBLAS 方法：
   
   特征值和特征向量
   
   
   • EigenTridiagonal DC — 使用分治算法（LAPACK 函数为 STEVD）计算对称三对角矩阵的特征值和特征向量。
   • EigenTridiagonalQR — 使用 QR 算法（LAPACK 函数为 STEV）计算对称三对角矩阵的特征值和特征向量。
   • EigenTridiagonalRobust — 使用MRRR（多相对鲁棒表示）算法（LAPACK 函数为 STEVR）计算对称三对角矩阵的特征值和特征向量。
   • EigenTridiagonalBisect — 使用二分法（LAPACK 函数为 STEVX）计算对称三对角矩阵的特征值和特征向量。

   
   矩阵缩减

   • ReduceToBidiagonal — 通过正交变换将一般实数或复数 m 乘 n 矩阵 A 简化为上或下双对角形式 B：Q**T * A * P = B。如果 m≥n，则 B 为上双对角矩阵；否则，B 为下双对角矩阵。(LAPACK 函数为 GEBRD）。
   • ReflectBidiagonalToQP — 将实数或复数矩阵 A 还原为对角线形式时，生成由 ReduceToBidiagonal 方法确定的正交矩阵 Q 和 P**T（或复数类型的 P**H）：A = Q * B * P**T. Q 和 P**T 分别定义为基本反射器 H(i) 或 G(i) 的乘积。(LAPACK 函数为 ORGBR、UNGBR）。
   • ReduceSymmetricToTridiagonal — 通过正交相似变换将实对称或复厄米矩阵 A 简化为三对角形式 B：Q**T * A * Q = B。(LAPACK 函数为 SYTRD、HETRD）。
   • ReflectTridiagonalToQ — 生成正交矩阵 Q，该矩阵被定义为 n 阶 n-1 个基本反射器的乘积，由 ReduceSymmetricToTridiagonal 返回。
     
     
   线性方程
   
   
   • LinearEquationsSolution — 计算具有平方系数矩阵 A 和多个右手系线性方程组的解。
   • LinearEquationsSolutionTriangular — 计算具有正三角形系数矩阵 A 和多个右手系线性方程组的解。
   • LinearEquationsSolutionSy — 计算具有对称或赫米梯共轭矩阵 A 和多个右手系线性方程组的解。
     
   • LinearEquationsSolutionComplexSy — 计算具有复对称矩阵 A 和多个右手系线性方程组的解。
   • LinearEquationsSolutionGeTrid — 计算具有对称或赫米特共轭正定矩阵 A 和多个右手系线性方程组的解。
   • LinearEquationsSolutionSyPD — 计算具有一般（非对称）三对角系数矩阵 A 和多个右手系线性方程组的解。
   • LinearEquationsSolutionSyTridPD — 计算具有对称三对角正定系数矩阵 A 和多个右手系线性方程组的解。
   
   正交分解
   
   
   • FactorizationQR — 计算一般 m×n 矩阵的 QR 分解：A = Q * R（LAPACK 函数为 GEQRF）。
   • FactorizationQRNonNeg — 计算 m×n 矩阵的 QR 分解：A = Q * R，其中 R 是对角线项为非负的上三角矩阵（LAPACK 函数为 GEQRFP）。
   • FactorizationQRPivot - 计算一般 m-by-n 矩阵的 QR 分解，并进行列透视：A * P = Q * R（LAPACK 函数为 GEQP3）。
   • FactorizationLQ — 计算一般 m×n 矩阵的 LQ 分解：A = L * Q（LAPACK 函数为 GELQF）。
   • FactorizationQL — 计算一般 m×n 矩阵的 QL 分解：A = Q * L（LAPACK 函数为 GEQLF）。
   • FactorizationRQ — 计算一般 m×n 矩阵的 RQ 分解：A = R * Q（LAPACK 函数为 GERQF）。
   
   矩阵因式分解
   
   
   • FactorizationPLU — 对 M 乘 N 的普通矩阵 A 进行 LU 因式分解，计算时使用部分透视和行间交换（LAPACK 函数为 GETRF）。
   • FactorizationPLUGeTrid — 使用带部分透视和行交换的消元法（LAPACK 函数为 GTTRF）计算一般（非对称）N 乘 N 三对角矩阵 A 的 LU 因式分解。
   • FactorizationLDL — 使用 Bunch-Kaufman 对角透视法（LAPACK 函数为 SYTRF 和 HETRF）计算实对称或复赫米特矩阵 A 的因式分解。
   • FactorizationLDLSyTridPD — 计算对称正定三对角矩阵 A 的因式分解（LAPACK 函数为 PTTRF）。
   • FactorizationCholesky — 计算实对称或复赫米特正定矩阵 A 的因式分解（LAPACK 函数为 POTRF）。
   • FactorizationCholeskySyPS — 计算实对称（复赫米特）正半定 n-by-n 矩阵（LAPACK 函数为 PSTRF）的带完全透视的 Cholesky 因式分解。
   
   
4. 添加了 Random 函数和方法，用于用随机值填充向量和矩阵。随机值在指定范围内均匀生成。
   

   static vector vector::Random(
     const ulong   size,       // vector length
     const double  min=0.0,    // min value
     const double  max=1.0     // max value
      );
   
   static matrix matrix::Random(
     const ulong   rows,       // number of rows
     const ulong   cols        // number of columns
     const float   min=0.0,    // min value
     const float   max=1.0     // max value
      );

5. 添加了对整数类型其它别名的支持。这将简化从 C 和 C++ 等其他语言的代码移植。
   
   这些别名不会引入新类型，而是为 MQL5 中的现有类型提供替代名称。它们可以在基础类型适用的所有环境中使用。
   
   
   • int8_t
   • uint8_t
   • int16_t
   • uint16_t
   • int32_t
   • uint32_t
   • int64_t
   • uint64_t
   
   
6. 添加了用于检测终端配色方案的新函数：
   
   
   • 新的属性 TERMINAL_COLORTHEME_NAME 已添加到 ENUM_TERMINAL_INFO_STRING 枚举中。将此属性与 TerminalInfoString 函数一起使用来查询终端的配色方案。可能值：Light（浅色） 和 Dark（深色）。
   • 新属性 THEME_COLOR_* 已添加到 ENUM_TERMINAL_INFO_INTEGER 枚举。将它们与 TerminalInfoInteger 函数一起使用来获取特定 UI 元素的颜色。
   
   要检测配色方案的变化，请使用 OnChartEvent 处理函数。当主题改变时，CHARTEVENT_CHART_CHANGE 事件会被触发两次。
   
   
7. 修正了编译包含 Array::Reserve 方法的代码时导致 MetaEditor 崩溃的错误。"Reserve" 方法不会改变数组大小，但会为指定数量的元素保留空间，以防止在添加新元素时重新分配内存。
8. 修正了 Array::Push 方法的行为，该方法用于在数组末尾添加新元素。该问题出现在具有预分配缓冲区空间的数组中。
9. 解决了与 OpenCL 协同工作的函数问题。

1. 加速了交易策略的优化。
2. 修正了一个 Bug，在某些情况下，该 Bug 会导致测试器代理在执行来自 MQL5 云网络的任务时占用过多内存。
   
   

网页端